Sponsor Area
Surface Areas and Volumes
Construct an angle of 90° at the initial point of a given ray and justify the construction.
Given: A ray OA.
Required: To construct an angle of 90° at O and justify the construction.
Steps of Construction:
1. Taking O as centre and some radius, draw an arc of a circle, which intersects OA, say at a point B.
2. Taking B as centre and with the same radius as before, draw an are intersecting the previously drawn are, say at a point C.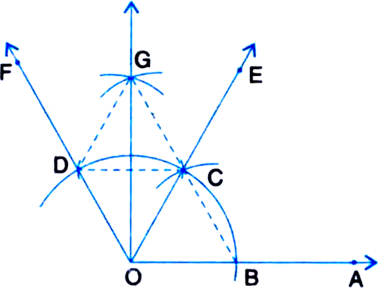
3. Taking C as centre and with the same radius as before, draw an arc intersecting the arc drawn in step 1, say at D.
4. Draw the ray OE passing through C. Then ∠EOA = 60°.
5. Draw the ray OF passing through D. Then ∠FOE = 60°.
6. Next, taking C and D as centres and with the radius more than ![]() ID, draw arcs to intersect each other, say at G.
ID, draw arcs to intersect each other, say at G.
7. Draw the ray OG. This ray OG is the bisector of the angle ∠FOE, i.e., ∠FOG![]()
Justification:
(i) Join BC.
Then. OC = OB = BC (By construction)
∴ ∆COB is an equilateral triangle.
∴ ∠COB = 60°.
∴ ∠EOA = 60°.
(ii) Join CD.
Then, OD = OC = CD (By construction)
∴ ∆DOC is an equilateral triangle.
Construct an angle of 45° at the initial point of a given ray and justify the construction.
Given: A ray OA.
Required: To construct an angle of 45° at O and justify the construction.
Steps of Construction:
1. Taking O as centre and some radius, draw an arc of a circle, which intersects OA, say at a point B.
2. Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C.
3. Taking C as centre and with the same radius as before, draw an arc intersecting the arc drawn in step 1, say at D.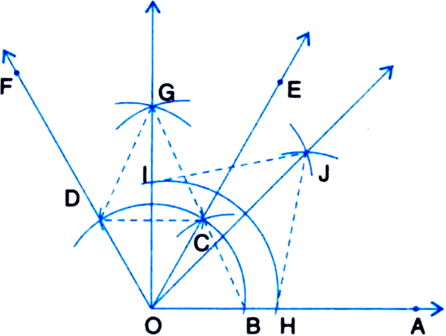
4. Draw the ray OE passing through C. Then ∠EOA = 60°.
5. Draw the ray OF passing through D. Then ∠FOE = 60°.
6. Next, taking C and D as centres and with radius more than ![]() CD, draw arcs to intersect each other, say at G.
CD, draw arcs to intersect each other, say at G.
7. Draw the ray OG. This ray OG is the bisector of the angle FOE, i.e., ∠FOG![]()
8. Now, taking O as centre and any radius, draw an arc to intersect the rays OA and OG. say at H and I respectively.
9. Next, taking H and I as centres and with the radius more than ![]() HI, draw arcs to intersect each other, say at J.
HI, draw arcs to intersect each other, say at J.
10. Draw the ray OJ. This ray OJ is the required bisector of the angle GOA.
Justification:
(i) Join BC.
Then, OC = OB = BC (By construction)
∴ ∆COB is an equilateral triangle.
∴ ∠COB = 60°.
∴ ∠EOA = 60°.
(ii) Join CD.
Then, OD = OC = CD (By construction)
∴ ∆DOC is an equilateral triangle.
∴ ∠DOC = 60°.
∴ ∠FOE = 60°.
(iii) Join CG and DG.
In ∆ODG and ∆OCG,
OD = OC | Radi fo the same arc
DG = CG | Arcs of equal radii
OG = OG | Common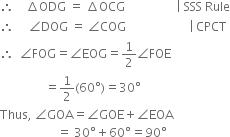
(iv) Join HJ and IJ![]()
OI = OH | Radii of the same arc
IJ = HJ | Arcs of equal radii
OJ=OJ | Common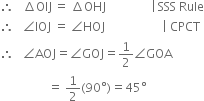
Construct the angles of the following measurements:

(i) 30°
Given: A ray OA.
Required: To construct an angle of 30° at O.
Steps of Construction:
1. Taking O as centre and some radius, draw an arc of a circle, which intersects OA, say at a point B.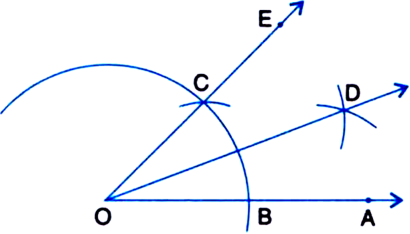
2. Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C.
3. Draw the ray OE passing through C. Then ∠EOA = 60°.
4. Taking B and C as centres and with the radius more than ![]() BC, draw arcs to intersect each other, say at D.
BC, draw arcs to intersect each other, say at D.
5. Draw the ray OD. This ray OD is the bisector of the angle EOA, i.e.,
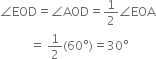
Construct the angles of the following measurements:
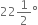
![]()
Given : A rayOA
Required : To construct an angle of ![]() at 0.
at 0.
Steps of Construction:
1. Taking O as centre and some radius, draw an arc of a circle, which intersects OA, say at a point B.
2. Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C.
3. Taking C as centre and with the same radius as before, draw an arc intersecting the arc drawn in step 1, say at D.
4. Draw the ray OE passing through C. Then ∠EOA = 60°.
5. Draw the ray OF passing through D. Then ∠FOE = 60°.
6. Next, taking C and D as centres and with radius more than ![]() CD, draw arcs to intersect each other, say at G.
CD, draw arcs to intersect each other, say at G.
7. Draw the ray OG. This ray OG is the bisector of the angle FOE, i.e.,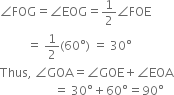
8. Now, taking O as centre and any radius, draw an arc to intersect the rays OA and OG, say at H and I respectively.
9. Next, taking H and I as centres and with the radius more than ![]() HI, draw arcs to intersect each other, say at J.
HI, draw arcs to intersect each other, say at J.
10. Draw the ray OJ. This ray OJ is the bisector of the angle GOA.
11. Now, taking O as centre and any radius, draw an arc to intersect the rays OA and OJ, say at K and L respectively.
12. Next, taking K and L as centres and with the radius more than ![]() KL, draw arcs to intersect each other, say at M.
KL, draw arcs to intersect each other, say at M.
13. Draw the ray OM. This ray OM is the bisector of the angle AOJ, i.e., ∠JOM = ∠AOM![]()
Sponsor Area
Mock Test Series
Mock Test Series





