Let the common ratio between the angles be x. Therefore, the angles will be 3x, 5x, 9x, and 13x respectively.

As the sum of all interior angles of a quadrilateral is 360º,

∴ 3x + 5x + 9x + 13x = 360º

30x = 360º

x = 12º

Hence, the angles are

3x = 3 × 12 = 36º

5x = 5 × 12 = 60º

9x = 9 × 12 = 108º

13x = 13 × 12 = 156º

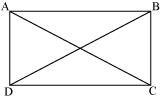
Let ABCD be a parallelogram. To show that ABCD is a rectangle, we have to prove that one of its interior angles is 90º.

In ΔABC and ΔDCB,

AB = DC (Opposite sides of a parallelogram are equal)

BC = BC (Common)

AC = DB (Given)

∴ ΔABC ≅ ΔDCB (By SSS Congruence rule)

⇒ ∠ABC = ∠DCB

It is known that the sum of the measures of angles on the same side of transversal is 180º.

∠ABC + ∠DCB = 180º (AB || CD)

⇒ ∠ABC + ∠ABC = 180º

⇒ 2∠ABC = 180º

⇒ ∠ABC = 90º

Since ABCD is a parallelogram and one of its interior angles is 90º, ABCD is a rectangle.

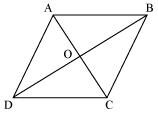
Let ABCD be a quadrilateral, whose diagonals AC and BD bisect each other at right angle i.e., OA = OC, OB = OD, and ∠AOB = ∠BOC = ∠COD = ∠AOD = 90º. To prove ABCD a rhombus, we have to prove ABCD is a parallelogram and all the sides of ABCD are equal.

In ΔAOD and ΔCOD,

OA = OC (Diagonals bisect each other)

∠AOD = ∠COD (Given)

OD = OD (Common)

∴ ΔAOD ≅ ΔCOD (By SAS congruence rule)

∴ AD = CD (1)

Similarly, it can be proved that

AD = AB and CD = BC (2)

From equations (1) and (2),

AB = BC = CD = AD

Since opposite sides of quadrilateral ABCD are equal, it can be said that ABCD is a parallelogram. Since all sides of a parallelogram ABCD are equal, it can be said that ABCD is a rhombus.

Let ABCD be a square. Let the diagonals AC and BD intersect each other at a point O. To prove that the diagonals of a square are equal and bisect each other at right angles, we have to prove AC = BD, OA = OC, OB = OD, and ∠AOB = 90º.

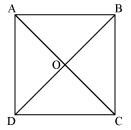
In ΔABC and ΔDCB,

AB = DC (Sides of a square are equal to each other)

∠ABC = ∠DCB (All interior angles are of 90$°$)

BC = CB (Common side)

∴ ΔABC ≅ ΔDCB (By SAS congruency)

∴ AC = DB (By CPCT)

Hence, the diagonals of a square are equal in length.

In ΔAOB and ΔCOD,

∠AOB = ∠COD (Vertically opposite angles)

∠ABO = ∠CDO (Alternate interior angles)

AB = CD (Sides of a square are always equal)

∴ ΔAOB ≅ ΔCOD (By AAS congruence rule)

∴ AO = CO and OB = OD (By CPCT)

Hence, the diagonals of a square bisect each other.

In ΔAOB and ΔCOB,

As we had proved that diagonals bisect each other, therefore,

AO = CO

AB = CB (Sides of a square are equal)

BO = BO (Common)

∴ ΔAOB ≅ ΔCOB (By SSS congruency)

∴ ∠AOB = ∠COB (By CPCT)

However, ∠AOB + ∠COB = 180º (Linear pair)

2∠AOB = 180º

∠AOB = 90º

Hence, the diagonals of a square bisect each other at right angles.