Sponsor Area
Areas of Parallelograms and Triangles
In quadrilateral ACBD, AC = AD and AB bisects ∠A (see figure). Show that ∆ABC ≅ ∆ABD. What can you say about BC and BD?
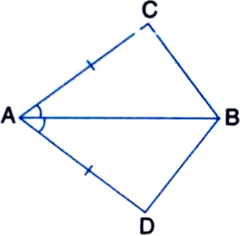
Given: In quadrilateral ACBD, AC = AD and AB bisects ∠A.
To Prove: ∆ABC ≅ ∆ABD.
Proof: In ∆ABC and ∆ABD,
AC = AD | Given
AB = AB | Common
∠CAB = ∠DAB
| ∵ AB bisects ∠A
∴ ∠ABC ≅ ∠ABD | SAS Rule
∴ BC = BD | C.P.C.T,
ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (see figure). Prove that:
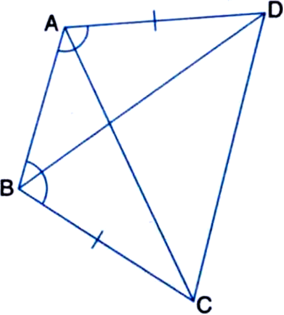
(i) ∆ABD ≅ ∆BAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC.
Given: ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA.
To Prove: (i) ∆ABD ≅ ∆BAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC.
Proof: (i) In ∆ABD and ∆BAC,
AD = BC | Given
AB = BA | Common
∠DAB = ∠CBA | Given
∴ ∆ABD ≅ ∠BAC | SAS Rule
(ii) ∵ ∆ABD ≅ ∆BAC | Proved in (i)
∴ BD = AC | C.P.C.T.
(iii) ∵ ∆ABD ≅ ∠BAC | Proved in (i)
∴ ∠ABD = ∠BAC. | C.P.C.T.
AD and BC are equal perpendiculars to a line segment AB (see figure). Show that CD bisects AB.
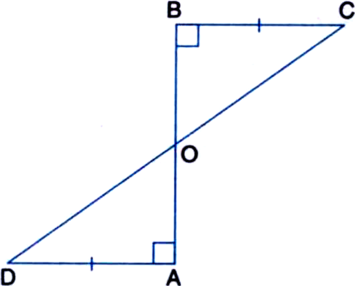
Given: AD and BC are equal perpendiculars to a line segment AB.
To Prove: CD bisects AB.
Proof: In ∆O AD and ∆OBC
AD = BC | Given
∠OAD = ∠OBC | Each = 90°
∠AOD = ∠BOC
| Vertically Opposite Angles
∴ ∠OAD ≅ ∆OBC | AAS Rule
∴ OA = OB | C.P.C.T.
∴ CD bisects AB.
I and m are two parallel lines intersected by another pair of parallel lines p and q (see figure). Show that ∆ABC ≅ ∆CDA.
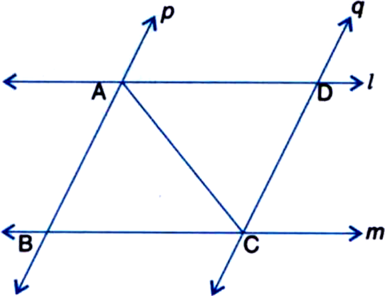
Given: I and m are two parallel lines intersected by another pair of parallel lines p and q.
To Prove: ∆ABC ≅ ∆CDA.
Proof: ∵ AB || DC
and AD || BC
∴ Quadrilateral ABCD is a parallelogram.
| ∵ A quadrilateral is a parallelogram if both the pairs of opposite sides are parallel
∴ BC = AD ...(1)
| Opposite sides of a ||gm are equal
AB = CD ...(2)
| Opposite sides of a ||gm are equal
and ∠ABC = ∠CDA ...(3)
| Opposite angles of a ||gm are equal
In ∆ABC and ∆CDA,
AB = CD | From (2)
BC = DA | From (1)
∠ABC = ∠CDA | From (3)
∴ ∆ABC ≅ ∆CDA. | SAS Rule
Sponsor Area
Mock Test Series
Mock Test Series





