Sponsor Area
Differential Equations
At any point (x, y) of a curve, the slope of the tangent is twice the slope of the line segment joining the point of contact to the point (– 4, – 3). Find the equation of the curve given that it passes through ( 2, 1).
Let y = f(x) be equation of curve.
Now 
is the slope of the tangent to the curve at the point (x, y)
From the given condition,
Separating the variables, we get,
Integrating, 
...(1)
Since curve passe through (-2, 1)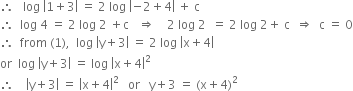
which is required equation of curve.
Find the equation of the curve passing through the point 
whose differential equation is sin x cos y dx + cos x sin y dy = 0.
The given differential equation is
sin x cos y dx + cos x sin y dy = 0
or sin x cos y dx = - cos x sin y dy
Integrating 
Since the curve passes through 
Find the equation of a curve passing through the point (0, 0) and whose differential equation is y' = ex sin x.
The given differential equation is
y' = ex sin x or 
Separating the variables, we get,
Integrating, 
...(1)
Now curve passes through (0, 0)
The volume of spherical balloon being inflated changes at a constant rate. If initially its radius is 3 units and after 3 seconds it is 6 units. Find the radius of balloon after t seconds.
Let v be volume of spherical balloon of radius r.
...(1)
From given condition,
Separating the variables and integrating, we get.
...(2)
Now t = 0 when r = 3
...(3)
Again t = 3 when r = 6
Putting 
Sponsor Area
Mock Test Series
Mock Test Series