Sponsor Area
Waves
Three sound waves of equal amplitudes have frequencies (ν – 1), ν, (ν + 1). They superpose to give beats. The number of beats produced per second will be.
-
4
-
3
-
2
-
1
C.
2
p1 =po sin 2π(x- 1)t
p2 =po sin 2π(x)t
p3 =po sin 2π(x+ 1)t
p=p1+p3+p2
=posin2π(x-1)t +po sin 2π(x+1)t +po sin 2π(x)t
= 2posin2πxtcos2πt +posin2πxt
= 2posin2πxt[2cos πt +1]
⇒ fbeat = 2
A wave travelling along the x-axis is described by the equation y(x, t) = 0.005 cos (αx −βt). If the wavelength and the time period of the wave are 0.08 m and 2.0 s, respectively, then α and β in appropriate units are
-
α = 25.00 π, β = π
-
α = 0.08/ π, 2.0/π
-
α = 0.04 / π , β =1.0/π
-
α = 12.50 , β =π/ 2.0
A.
α = 25.00 π, β = π
y = 0.005 cos (αx − βt)
comparing the equation with the standard form,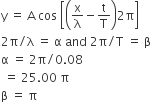
A whistle producing sound waves of frequencies 9500 Hz and above is approaching a stationary person with speed v ms−1. The velocity of sound in air is 300 ms−1. If the person can hear frequencies upto a maximum of 10,000 Hz, the maximum value of v upto which he can hear the whistle is
-

-

-
15 ms-1
-
30 ms-1
C.
15 ms-1

When two tuning forks (fork 1 and fork 2) are sounded simultaneously, 4 beats per second are heard. Now, some tape is attached on the prong of the fork 2. When the tuning forks are sounded again, 6 beats per seconds are heard. If the frequency of fork 1 is 200 Hz, then what was the original frequency of fork 2?
-
200 Hz
-
202 Hz
-
196 Hz
-
204 HN
C.
196 Hz
|f1−f2| =4 Since mass of second tuning fork increases so f2 decrease and beats increase so f1>f2 ⇒ f2=f1−4 = 196
Sponsor Area
Mock Test Series
Mock Test Series





