Wired Faculty
Sponsor Area
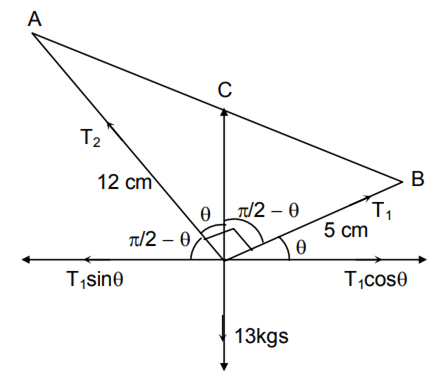
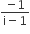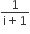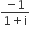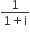If the roots of the equation bx2+ cx + a = 0 be imaginary, then for all real values of x, the expression 3b2x2 + 6bcx + 2c2 is
greater than 4ab
less than 4ab
greater than -4ab
less than 4ab
C.
greater than -4ab
As, bx2 + cx + a = 0 has imaginary roots
So, c2< 4ab
Now, 3b2x2 + 6bcx + 2c2
= 3(bx + c)2– c2≥ – c2≥ – 4ab
The conjugate of a complex number is 
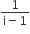. Then the complex number is
C.
The quadratic equations x2 – 6x + a = 0 and x2 – cx + 6 = 0 have one root in common. The other roots of the first and second equations are integers in the ratio 4 : 3. Then the common root is
1
4
3
2
D.
2
Let α and 4β be roots of x2– 6x + a = 0 and
α, 3β be the roots of x2– cx + 6 = 0, then
α + 4β = 6 and 4αβ = a
α + 3β = c and 3αβ = 6.
We get αβ = 2 ⇒ a = 8
So the first equation is x2 – 6x + 8 = 0 ⇒ x = 2, 4
If α = 2 and 4β = 4 then 3β = 3
If α = 4 and 4β = 2, then 3β = 3/2 (non-integer)
∴ common root is x = 2.
A body weighing 13 kg is suspended by two strings 5 m and 12 m long, their other ends being fastened to the extremities of a rod 13 m long. If the rod be so held that the body hangs immediately below the middle point. The tensions in the strings are
12 kg and 13 kg
5 kg and 5 kg
5 kg and 12 kg
5 kg and 13 kg
C.
5 kg and 12 kg
Sponsor Area
Mock Test Series
