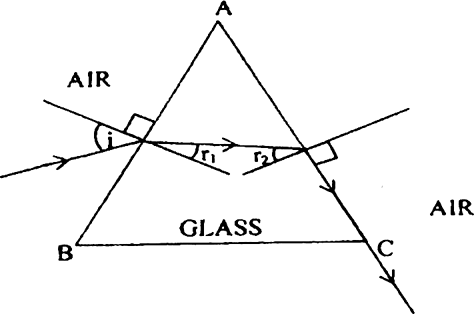
At what angle, a ray of light should be incident on the first face AB of a regular glass prism ABC so that the emergent ray grazes the adjacent face AC? See Figure 7 below. (Refractive Index of glass = 1.6)
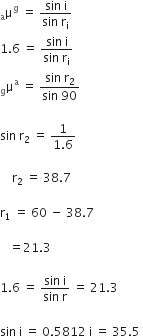

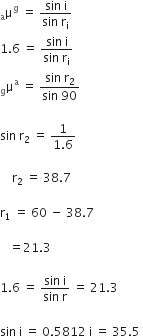
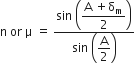

Here,
e= Angle of emergence
A = refracting angle
r + r’ = Angle of a refraction
δ = deviation
i + e = A + δ ---(i)
A = r1+ r2 ---(ii)
Above relation connecting i. c., A + δ are shown above.
Under minimum deviation i = e, rt = r2 = r
From Eq. (i), we have
2 i = A + δ min
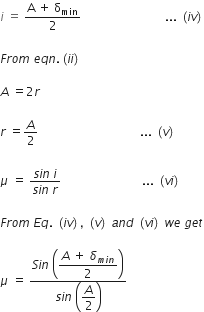
Hence proved.
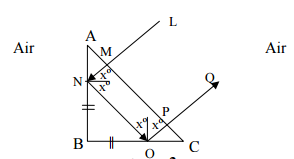
∠A =  C = 45°
C = 45°
∠ i = 45°
For total internal reflection to take place at faces,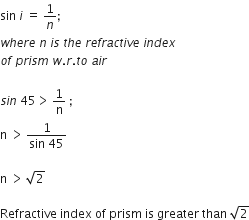
Given,
n = 1.6
sin = ?
We know,
n = 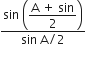
1.6 = 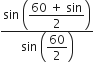
53.13 = 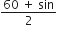
sin = 46.26o
Sponsor Area
Mock Test Series