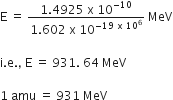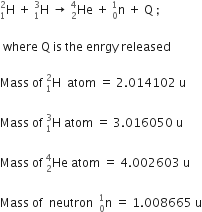Energy-Mass Equivalence : Nuclear Binding Energy

Mass defect : The difference between the sum of the mass of the nucleons constituting a nucleus and the rest mass of the nucleus is known as mass defect.
It is denoted by m.

Δm = sum of mass of nucleons - mass of nucleus.

Given,
Mass No. of heavy nucleus is A = 240 , and
binding energy/nucleon = 7.5 MeV

Therefore,
Total binding energy of nucleus = 240 x 7.6 Mev

                                         = 1824 MeV

It splits into two nuclei of Mass No. A¹ = 120.

Therefore,
Binding energy per nucleon = 8.5 MeV

∴ Total binding energy of two nuclei = 2 x 120 x 8.5 MeV

                                               = 2040 MeV.

∴ Disintegration energy Q = 2040 - 1824 MeV

                              Q = 216 MeV

We know that,
1 amu = 1.660565 x 10^-27kg

Energy equivalent to this mass, E = mc²

E = (1.660565 x 10-27) x (2.998 x 10⁸)²

E = 1.4925 x 10^-10J

Mass defect Δ m = Mass of reactant - Mass of product

Neutral temperature is independent of temp. of cold junction, hence neutral temp, will not change, if temp, of cold junction is lowered.

T, = 2 T_n T₀

If temp. of cold junction decreases, temperature of inversion increases.