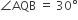एक पार्क में बने 5m त्रिज्या वाले वृत्त पर खड़ी तीन लड़कियाँ रेशमा, सलमा एवं मनदीप खेल रही हैं। रेशमा एक गेंद को सलमा के पास, सलमा मनदीप के पास तथा मनदीप रेशमा के पास फेंकती है। यदि रेशमा तथा सलमा के बीच और सलमा तथा मनदीप के बीच की प्रत्येक दूरी 6 m हो, तो रेशमा और मनदीप के बीच की दूरी क्या है?
माना KR = x m
.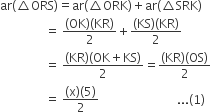

दोबारा, ar (∆ORS)
समीकरण (i) तथा (ii) के प्रयोग से: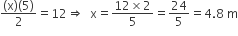
⇒ KR = 4.8 m
∴ RM = 2KR = 2 × (4.8) = 9.6 m
अत: रेशमा और मनदीप के बीच की दूरी 9.6 m है।







 खींचों।
खींचों।




 तथा
तथा 
 ज्ञात कीजिए।
ज्ञात कीजिए।



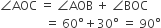

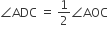
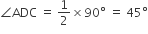

 और
और  .
.
 में,
में, एक समबाहु त्रिभुज है।
एक समबाहु त्रिभुज है। 
 और शेष भाग में
और शेष भाग में  अंतरित करती है।
अंतरित करती है।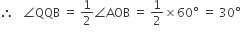
 शेष भाग में
शेष भाग में  अंतरित करती है।
अंतरित करती है।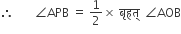

 और
और