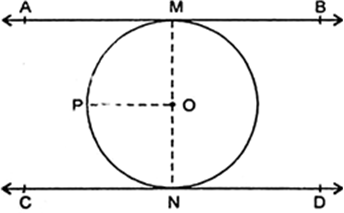
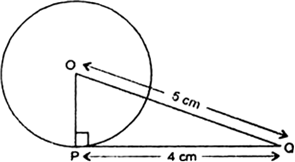
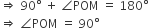यदि एक बिंदु P से O केंद्र वाले किसी वृत्त पर PA, PB स्पर्श रेखाएँ परस्पर  के कोण पर झुकी हों, तो
के कोण पर झुकी हों, तो  बराबर है:
बराबर है:
- 50°
- 60°
- 70°
- 80°
A.
50°ΔPOA और ΔPOB में,
PA = PB (बाह्य बिंदु से समान स्पर्श रेखाएँ)
OA = OB (वृत्त की त्रिज्याएँ)
और OP = OP (उभयनिष्ठ)
∴ ΔPOA ≅ ΔPOB (SSS सर्वांगसमता)
⇒ 
⇒ 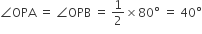
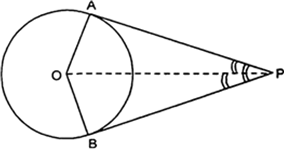
हम जानते हैं कि वृत्त की त्रिज्या और स्पर्श रेखा के बीच 90° का कोण होता है।
∴ 
अब ΔOAP में,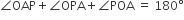
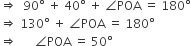






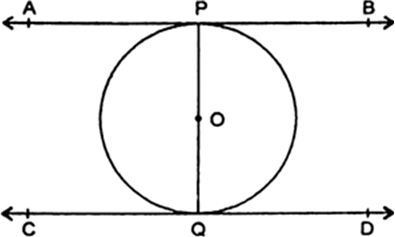
 = 90° ....(i)
= 90° ....(i) ...(ii)
...(ii) [∵ वैकल्पिक आंतरिक कोण]
[∵ वैकल्पिक आंतरिक कोण]