आकृति 5 में, सजावट के लिए बना एक ब्लाक दर्शाया गया है जो दो ठोसों-एक घन तथा एक अर्धगोले से बना है। ब्लाक का आधार एक 6 सेमी भुजा का घन है तथा उसके ऊपर एक अर्धगोला है जिसका ब्यास 3.5 सेमी है। ब्लाक का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए। 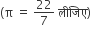
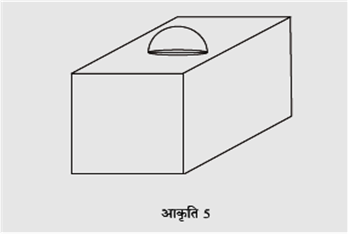

आकृति 5 में, सजावट के लिए बना एक ब्लाक दर्शाया गया है जो दो ठोसों-एक घन तथा एक अर्धगोले से बना है। ब्लाक का आधार एक 6 सेमी भुजा का घन है तथा उसके ऊपर एक अर्धगोला है जिसका ब्यास 3.5 सेमी है। ब्लाक का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए। 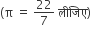


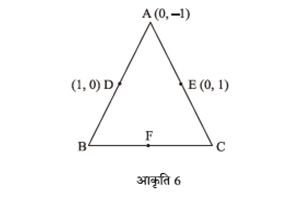
आकृति 6 में, बनी  ABC, जिसके शीर्ष A के निर्देशांक (0, -1) हैं तथा भुजाओं AB तथा AC के मध्य-बिंदुओं D तथा E के निर्देशांक क्रमशः (1, 0) तथा (0, 1) हैं। यदि F भुजा BC का मध्य-बिंदु हैं तो त्रिभुजों DEF तथा ABC के क्षेत्रफल ज्ञात कीजिए।
ABC, जिसके शीर्ष A के निर्देशांक (0, -1) हैं तथा भुजाओं AB तथा AC के मध्य-बिंदुओं D तथा E के निर्देशांक क्रमशः (1, 0) तथा (0, 1) हैं। यदि F भुजा BC का मध्य-बिंदु हैं तो त्रिभुजों DEF तथा ABC के क्षेत्रफल ज्ञात कीजिए।
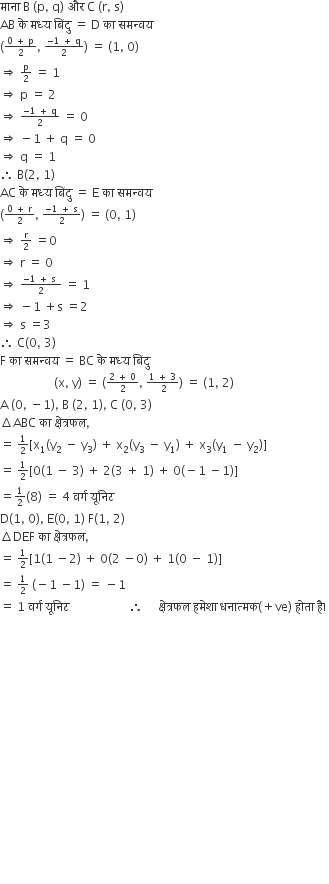
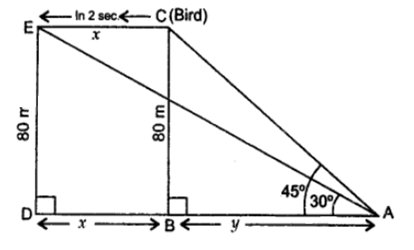
80 मी ऊँचे पेड़ के शिखर पर एक पक्षी बैठा है। धरती के एक बिंदु से पक्षी का उन्नयन कोण 450 है। पक्षी क्षैतिज रूप से इस प्रकार उड़ता है कि वह धरती से एक समान ऊँचाई पर रहता है। 2 से. की उड़ान के बाद पृथ्वी के उसी बिंदु से पक्षी का उन्नयन कोण 300 हो जाता है। पक्षी के उड़ने की चाल ज्ञात कीजिए। 

सिध्द कीजिए कि वृत्त जे बाह्म-बिंदु से वृत्त पर खींची गई स्पर्श रेखाएँ लम्बाई में सामान होती हैं।
दिया है,
PT और TQ दो स्पर्शरेखा हैं जो बाहरी बिंदु T से वृत्त C (O, r) में लिए गयीं हैं।
सिध्द कीजिए(to prove): 1. PT = TQ
2. ∠OTP = ∠OTQ
निर्माण: जोड़ना OT
प्रमाण(Proof): हम जानते हैं, कि वृत्त में स्पर्शरेखा संपर्क बिंदु के माध्यम से त्रिज्या के लिए लम्बवत्त है।
Sponsor Area
Mock Test Series