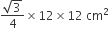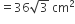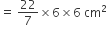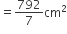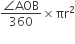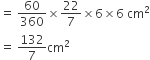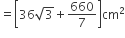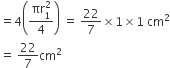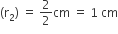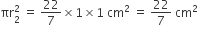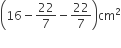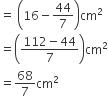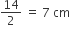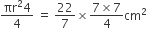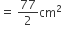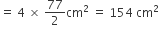आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि ABCD भुजा 14 cm का एक वर्ग है तथा APD और BPC दो अर्धवृत हैं।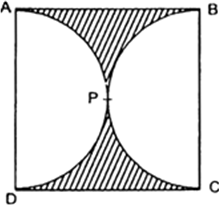
यहाँ पर, वर्ग ABCD की भुजा = 14 cm
वर्ग ABCD का क्षेत्रफल = भुजा x भुजा = (भुजा)2
= 14 x 14 cm2 = 196 cm2
प्रत्येक अर्धवृत की त्रिज्या (r) = 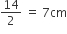
दोनों अर्धवृतों (APD + BPC) का क्षेत्रफल = 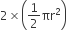
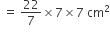
= 154 cm2
अत: आकृति के छायांकित भाग का क्षेत्रफल = (196 - 154) cm2
= 42 cm2






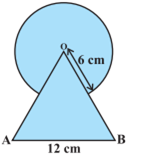
 समबाहु त्रिभुज है।
समबाहु त्रिभुज है।
 का क्षेत्रफल =
का क्षेत्रफल = 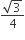 x (भुजा)2
x (भुजा)2