HCF (306, 657) = 9, दिया है तो LCM (306, 657) ज्ञात कीजिएl
HCF (306, 657) = 9
LCM (306, 657) = 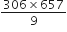
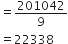
HCF (306, 657) = 9, दिया है तो LCM (306, 657) ज्ञात कीजिएl
HCF (306, 657) = 9
LCM (306, 657) = 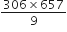
जाँच कीजिए कि क्या किसी प्राकृत संख्या के लिए संख्या 6n अंक 0 पर समाप्त हो सकती हैl
यदि 6n,  , शून्य अंक पर समाप्त होता है तो वह 5 से विभाज्य होगा अर्थात 6n के अभाज्य गुणनखंड अभाज्य संख्या 5 होगी यह सम्भव नहीं है, क्योंकि 6 के अभाज्य गुणनखंड 2 और 3 हैं और अंक गणित कि आधार भूत प्रमेय द्वारा 6n के अद्वितीय गुणनखंड इनके अतिरिक्त और गुणनखंड नहीं हो सकतेl
, शून्य अंक पर समाप्त होता है तो वह 5 से विभाज्य होगा अर्थात 6n के अभाज्य गुणनखंड अभाज्य संख्या 5 होगी यह सम्भव नहीं है, क्योंकि 6 के अभाज्य गुणनखंड 2 और 3 हैं और अंक गणित कि आधार भूत प्रमेय द्वारा 6n के अद्वितीय गुणनखंड इनके अतिरिक्त और गुणनखंड नहीं हो सकतेl
अत: 6 शून्य अंक पर समाप्त नहीं हो सकता जहाँ 
व्याख्या कीजिए कि 7 x 11 x 12 + 13 और 7 x 6 x 5 x 4 x 3 x 2 x 1 + 5 भाज्य संख्याएँ क्यों हैं?
कोई भी धनात्मक संख्या जिसके दो से ज्यादा गुणनखंड बनते है वह भाज्य संख्या होती है
7 × 11 × 13 + 13 = 13 × (7 × 11 + 1)
= 13 × 78
= 13 × 13 × 3 × 2
दी गई संख्या के दो से ज्यादा गुणनखंड है इसलिए यह एक भाज्य संख्या है
इसी तरह,
7 × 6 × 5 × 4 × 3 + 5
= 5 × (7 × 6 × 4 × 3 x 2 + 1)
= 5 × 1009
⇒ दी गई संख्या भाज्य संख्या है क्योंकि इसके दो से ज्यादा गुणनखंड बनते हैl
किसी खेल के मैदान के चारों ओर एक वृताकार पथ हैl इस मैदान का एक चक्कर लगाने में सोनिया को 18 मिनट लगते हैंl, जबकि इसी मैदान का एक चक्कर लगाने में रवि को 12 मिनट लगते हैंl मान लीजिए वह दोनों एक ही स्थान और एक ही समय पर चलना प्रारंभ करके एक ही दिशा में चलते हैंl कितने समय बाद वह पुन: प्रारंभिक स्थान पर मिलेंगे?
हम 18 और 12 का LCM ज्ञात करते हैl
हम प्राप्त करते है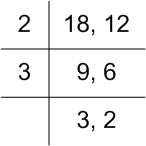
18 = 2 × 32
और 12 = 22 × 3
∴ 18 और 12 का LCM है 22 × 32 = 36.
अत: प्रांरभिक स्थान पर वे 36 मिनट बाद मिलेंगेl
Sponsor Area
Mock Test Series