निम्नलिखित संख्याओं का HCF ज्ञात करने के लिए यूक्लिड विभाजन का प्रयोग कीजिए:
(i)135 और 225 (ii) 196 और 38220 (iii) 867 और 255
(i) बड़े पूर्णांक से शुरू कीजिए अर्थात 225 विभाजन एल्गोरिथम का प्रयोग करते हुए हम प्राप्त करते हैं:![]()
अब 135 को भाज्य और 90 को भाजक मानकर दोबारा विभाजन एल्गोरिथम का प्रयोग करते हुए हम प्राप्त करते हैं:![]()
अब 90 को भाज्य और 45 को भाजक मानकर एक बार फिर विभाजन एल्गोरिथम का प्रयोग करते हुए हम प्राप्त करते हैं:![]()
अब शेषफल 0 प्राप्त हुआ है इसलिए हमारी प्रक्रिया समाप्त हुई
135 और 225 का HCF 45 हैl
(ii) अब 38220 को भाज्य और 196 को भाजक मानकर दोबारा विभाजन एल्गोरिथम का प्रयोग करते हुए हम प्राप्त करते हैं:![]()
अब शेषफल 0 प्राप्त हुआ है इसलिए हमारी प्रक्रिया समाप्त हुई
इसलिए 196 और 38220 का HCF 196 हैl
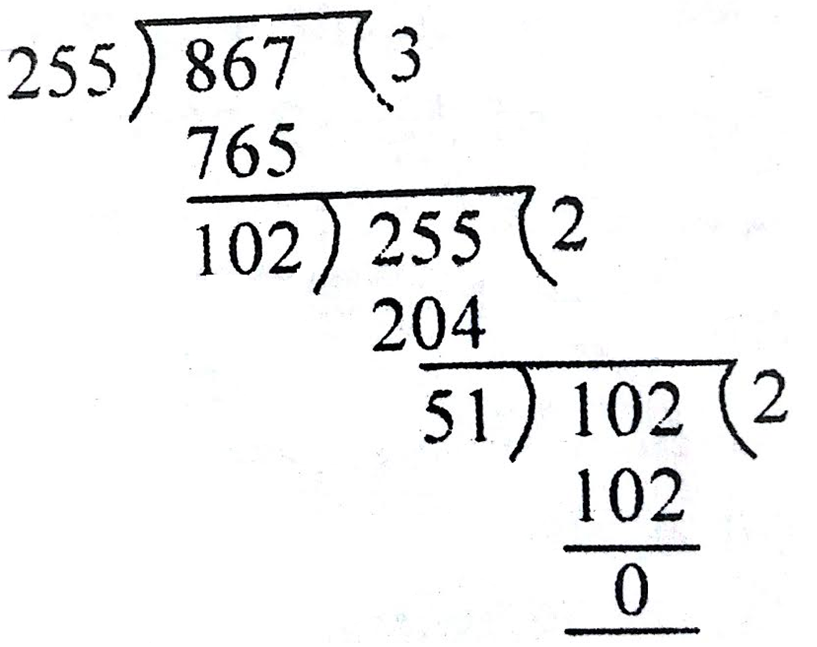
(iii) 867 = 255 x 3 + 102
255 = 102 x 2 + 51
102 = 51 x 2 + 0
अब शेष '0' रह गया है, इसलिए हमारी प्रक्रिया समाप्त हुई और
HCF (867, 255) = 51
जाँच: