Linear Programming

We are minimise and maximise
Z = 3x + 9 y
subject to constraints
x + 3 y ≤ 60
x + y ≥ 10
x ≤ y
x ≥ 0, y ≥ 0
Consider a set of rectangular cartesian axes OXY in the plane.
It is clear that any point which satisfies x ≥ 0, y ≥ 0 lies in the first quadrant.
Let us draw the graph of the line x + 3y = 60
For x = 0, 3 y = 60 or y = 20
For y = 0, x = 60
∴ line meets OX in A(60, 0) and OY in L(0, 20)
Let us draw the graph of
x + y = 10
For  x = 0, y = 10
For y = 0, x = 10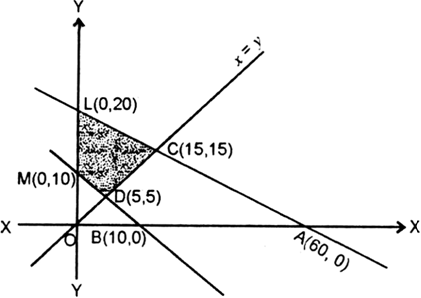

∴ line meets OX in B(10, 0) and OY in M(0, 10).
Again we draw the graph of x = y
This is a straight line passing through O and meeting AL in C(15, 15) and BM in D(5, 5).
Since feasible region is the region which satisfies all the constraints.
∴ DCLM is the feasible region, which is bounded. The corner points are D(5, 5), C(15, 15), L(0, 20), M(0, 10).
At D(5, 5), Z = 15 + 45 = 60
At C(15, 15), Z = 45 + 135 = 180
At L(0, 20), Z = 0 + 180 = 180
At M(0, 10), Z = 0 + 90 = 90
∴ minimum value = 60 at (5, 5)
and maximum value = 180 at (15, 15) or (0, 20).

Tips: -

We are to minimise and maximise Z = 5x + 10y subject to constraints x + 2 y ≤ 120
x + y ≥ 60
x - 2y ≥ 0
x, y ≥ 0
Consider a set of rectangular cartesian axes OXY in the plane.
It is clear that any point which satisfies x ≥ 0, y ≥ 0 lies in the first quadrant.
Let us draw the graph of x + 2 y = 120
For x = 0, 2 y = 120 or y = 60
For y = 0, x = 120
∴ line meets OX in A( 120, 0) and OY in L(0, 60).
Also we draw the graph of
x + y = 60.
For r = 0, y = 60
For y = 0, x = 60
∴ line meets OX in B(60, 0) and OY in L(0, 60).
Again we draw the graph of
x - 2y = 0
This is a line through the origin and C(40, 0), which is point of intersection of x - 2 y = 0 and x + y = 60

Since feasible region satisfies all the constraints.
∴ BADC is the feasible region.
Comer points are B(60, 0), A(120, 0), D(60, 30), C(40, 20).
At B(60, 0), Z = 300 + 0 = 300
At A(120, 0), Z = 600+ 0 = 600
At D(60, 30), Z = 300 + 300 = 600
At C(40, 20), Z = 200 + 200 = 400
∴ minimum value = 300 at (60, 0) and maximum value = 600 at (120, 0) and (60, 30).

We are to minimise
z = 5x + 7y
subject to the constraints
2x + y ≥ 8
x + 2y ≥ 10
x, y ≥ 0
Consider a set of rectangular cartesian axes OXY in the plane.
It is clear that any point which satisfies x ≥ 0, y ≥ 0 lies in the first quadrant.
Let us draw the graph of
2x + y = 8
For x = 0, y = 8
For y = 0, 2 x = 8 or x = 4
∴ line meets OX in A (4, 0) and OY in L (0, 8).

Again we draw the graph of
x + 2y = 10.
For x = 0, 2y = 10 or y = 5
For y = 0, x = 10
∴ line meets OX in B (10, 0) and OY in M (0, 5)
Since feasible region is the region which satisfies all the constraints
∴ shaded region is the feasible region and comer points are B (10, 0), C (2, 4), L (0, 8).
At B (10, 0), z = 5 (10) + 7 (0) = 50 + 0 = 50
At C (2, 4), z = 5 (2) +7 (4) = 10 + 28 = 38
At L (0, 8), z = 5 (0) + 7 (8) = 0 + 56 = 56
∴ 38 is the smallest value of z at (2, 4)
Since feasible region is unbounded
∴ we are to check whether this value is minimum.
For this we draw the graph of
5x + 7y < 38    ...(1)
Since (1) has no common point with feasible region.
∴ minimum value = 38 at (2, 4).

We are to minimise and maximise
Z = x + 2y subject to constraints x + 2y ≥ 100, 2x - y ≤ 0, 2x + y ≤ 200, x, y ≥ 0
Consider a set of rectangular cartesian axes OXY in the plane.
It is clear that any point which satisfies x ≥ 0, y ≥ 0 lies in the first quadrant.
Let us draw the graph of x + 2 y = 100
For x = 0, 2 y = 100 or y = 50
For y = 0, x = 100
∴  line meets OX in A(100, 0) and OY in L(0, 50).
2x - y = 0 is a straight line passing through origin and C(20, 4), which is point of intersection of 2x - y = 0 and x + 2y = 100.
Again we draw the graph of 2x + y = 200.
For x = 0, y = 200
For y = 0, 2x = 200 or x = 100
∴ line meets OX in A(100, 0) and OY in M(0, 200).
Since feasible region satisfies all the constraints.
∴ CDML is the feasible region.
The comer points are C(20, 40), D(50. 100), M(0, 200), L(0, 50).
At C(20, 40), Z = 20 + 80 = 100
At D(50, 100), Z = 50 + 200 = 250
At M(0, 200), Z = 0 + 400 = 400
At L(0, 50), Z = 0 + 100 = 100

∴  maximum value = 400 at (0, 200)
and minimum value = 100 at (20, 40) and (0, 50) i.e. along the segment joining (20, 40) and (0, 50).