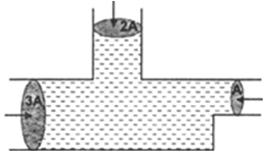
State and prove Pascal's law.
PAscal's law states that, if some pressure is applied at any point of incompressible liquid then the same pressure is transmitted to all the points of liquid and on the walls of the container.
Let us imagine an arbitrary right angled prismatic triangle in the liquid of density ρ. This prismatic element is very small so, every part is considered at the same depth from the liquid surface. Therefore, effect of gravity is the same at all these points. That, the small element is in equilibrium. 
The area of faces ABFE, ABDC and CDFE are ad, bd and cd respectively. Let the pressure of liquid on faces ABFE, ABDC and CDFE be P1, P2 and P3respectively.
The pressure of liquid exerts the force normal to the surface. Let us assume pressure P1exerts the force F1 on the surface ABFE, pressure P2 exerts force F2 on the surface ABDC and pressure P3 exerts force on the surface CDFE.
So, Force F1 is given by,
Since the prism is in equilibrium, so net force on the prism is zero.
Thus,