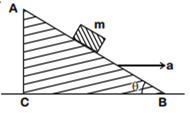
Which one of the following statements is incorrect?
Rolling friction is smaller than sliding friction.
Limiting value of static friction is directly proportional to normal reaction.
Coefficient of sliding friction has dimensions of length.
Frictional force opposes the relative motion.
C.
Coefficient of sliding friction has dimensions of length.
Coefficient of friction or sliding friction has no dimension.