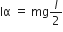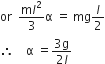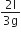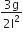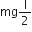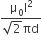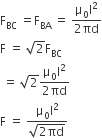A uniform rod of length l and mass m is free to rotate in a vertical plane about A. The rod initially in horizontal position is released. The initial angular acceleration of the rod is: (Moment of inertia of rod about A is 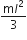 )
)
A.

The moment of inertia of the uniform rod about an axis through the end and perpendicular to length is
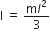
where m is mass of rod and l its length.
Torque  acting on centre of gravity of rod is given by
acting on centre of gravity of rod is given by
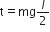
or