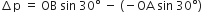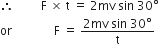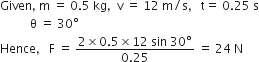Question
A block B is pushed momentarily along a horizontal surface with an initial velocity v. if μ is the coefficient of sliding friction between B and the surface, block B will come to rest after a time:
-
v/gμ
-
gμ/v
-
g/v
-
v/g
Solution
A.
v/gμ
Block B will come to rest, if force applied to it will vanish due to frictional force acting between block B and surface, ie,
force applied = frictional force
i.e., μmg = ma
μmg = m (v/t)
t =v/μg
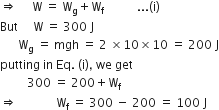
represents the momentum of the object before the collision, and the vector 
that after the collision. The vector 
represents the change in momentum of the object 
. 
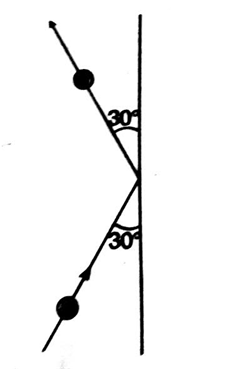
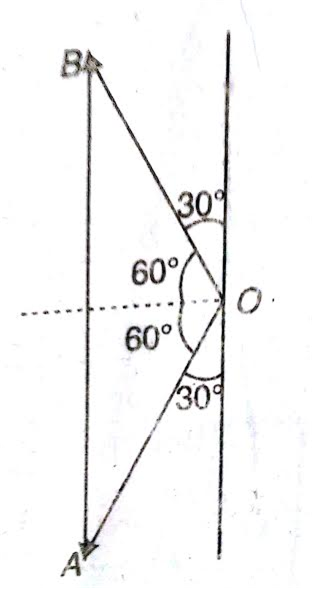
are equal, the components of 
along the wall are equal and in the same direction, while those perpendicular to the wall are equal and opposite. Thus, the change in momentum is due only to the change in direction of the perpendicular components.
