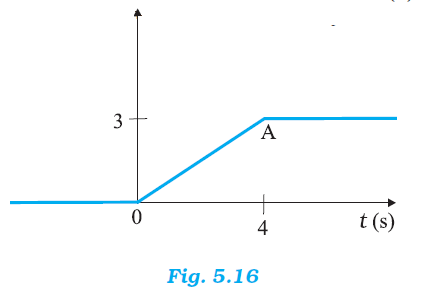
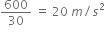Figure 5.16 shows the position-time graph of a particle of mass 4 kg. What is the (a) force on the particle for t < 0, t> 4 s,0 < t < 4 s? (b) impulse at t = 0 and t = 4 s? (Consider one-dimensional motion only).
For t < 0
That is, the displacement of the particle in this time interval is zero. Hence, the force acting on the particle is zero.
For t > 4 s
In the given graph, the position of the particle is parallel to the time axis. It indicates that the particle is at rest at a distance of 3 m from the origin. Hence, no force is acting on the particle.
For 0 < t < 4
The position-time graph has a constant slope in the given graph.
Hence, the acceleration produced in the particle is zero.
(b)
At t = 0,
Impulse = Change in momentum
= mv – mu
Mass of the particle, m = 4 kg
Initial velocity of the particle, u = 0
Final velocity of the particle, v =
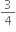 m/s
m/s∴ Impulse = 4 x (
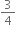 - 0)
- 0)= 3 kg m/s
At t = 4 s,
Initial velocity of the particle, u =
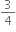 m/s
m/s Final velocity of the particle, v = 0
∴ Impulse = 4 (0 -
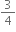 ) = -3 kg m/s
) = -3 kg m/s
For t > 4 s
It can be observed from the given graph that the position of the particle is parallel to the time axis. It indicates that the particle is at rest at a distance of
3 m from the origin. Hence, no force is acting on the particle.
For 0 < t < 4
It can be observed that the given position-time graph has a constant slope. Hence, the acceleration produced in the particle is zero. Therefore, the force acting on the particle is zero.
(b) At t = 0
Impulse = Change in momentum
= mv – mu
Mass of the particle, m = 4 kg
Initial velocity of the particle, u = 0
Final velocity of the particle, v =
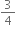 m/s
m/s ∴ Impulse = 4 (
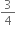 - 0) = 3 kg m/s
- 0) = 3 kg m/sAt t = 4 s,
Initial velocity of the particle, u = m/s
Final velocity o9f the particle, v = 0
∴ Impulse = 4 (0 -
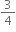 ) = -3 kg m/s
) = -3 kg m/s 





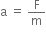 =
=