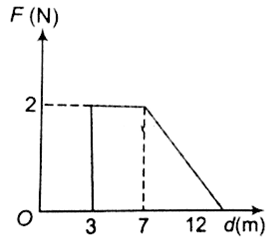
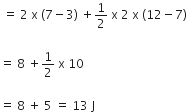
Force F on a particle moving in a straight line varies with distance d as shown in the figure. The work done on the particle during its displacement of 12 m is
21 J
26 J
13 J
18 J
C.
13 J
Work done = Area under (F - x) graph
= 2 x (7-3) +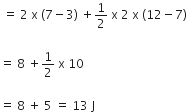 
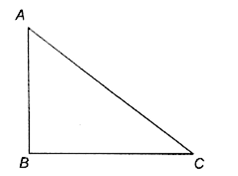
Uniform magnetic field acting along AB. If the magnetic force on the arm BC Is F, the force on the arm AC is
A.
-F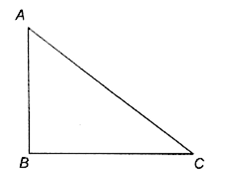
Two stone of masses m and 2m are whirled in horizontal circles, the heavier one in a radius r/2 and the lighter one in radius r. The tangential speed of lighter one in radius r. The tangential speed of lighter stone is n times that of the value of heavier stone when they experience same centripetal forces. The value of n is
2
3
4
1
A.
2
Given, that two stones of masses m and 2m are whirled in horizontal circles, the heavier one in a radius r/2 and lighter one in radius r as shown in a figure.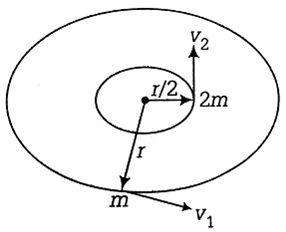
As lighter stone is n times that of the value of heavier stone when they experience same centripetal forces, we get
(Fc)heavier = (Fc)lighter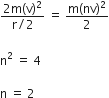
Two identical piano wires kept under the same tension T have a fundamental frequency of 600 Hz. The fractional increase in the tension of one of the wires which will lead to occurrence of 6 beats/s when both the wires oscillate together would be
0.02
0.03
0.04
0.01
A.
0.02
According to law of tension, the frequency of the string varies directly as the square root of its tension
Sponsor Area
Mock Test Series
