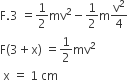Laws of Motion

The upper half of an inclined plane with inclination φ is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half is given by

• 2sinφ

• 2cosφ

• 2tanφ

• tanφ

A bullet fired into a fixed target loses half of its velocity after penetrating 3 cm. How much further it will penetrate before coming to rest assuming that it faces constant resistance to motion?

• 3.0 cm

• 2.0 cm

• 1.5 cm

• 1.0 cm

Out of the following pair, which one does NOT have identical dimensions is

• angular momentum and Planck’s constant

• impulse and momentum

• moment of inertia and moment of a force

• work and torque

A body A of mass M while falling vertically downwards under gravity breaks into two parts; a body B of mass 1/3 M and a body C of mass 2/3 M. The centre of mass of bodies B and C taken together shifts compared to that of body A towards

• depends on height of breaking

• does not shift

• body C

• body B