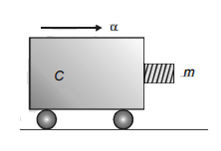
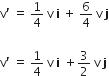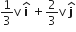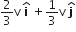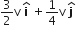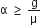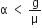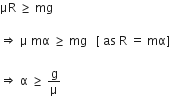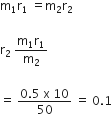A mass m moving horizontally (along the x -axis) with velocity v collides and sticks to mass of 3m moving vertically upward (along the y -axis) with velocity 2v. The final velocity of the combination
A.
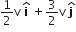
From the law of conservation of linear momentum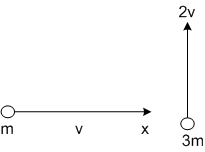
mv + (3m)(2v) = (4m)v'
mv i + 6mv j = 4 mv'
A block of mass m is in contact with the cart C as shown in the figure
The coefficient of static friction between the block and the cart is μ. The acceleration α of the cart that will prevent the block from falling satisfies
C.
When a cart moves with some acceleration toward right then a pseudo force (mα) acts on block towards left. The force (mα) is action force by a block on the cart. Now, block will remain static w.r.t cart if frictional force 
A ball moving with velocity 2 ms-1 collides head on with another stationary ball of double the mass. If the coefficient of restitution is 0.5, then their velocities (in ms-1) after collision will be
0,1
1,1
1,0.5
0,2
A.
0,1
If two bodies collide head on with coefficient of restitution
A man of 50 kg mass standing in a gravity free space at height of 10 m above the floor. He throws a stone of 0.5 kg mass downwards with a speed 2 ms-1. When the stone reaches the floor, the distance of the man above the floor will be
9.9 m
10.1
10 m
20 m
B.
10.1
m r = constant
The distance of the man above the floor (total height) = 10+0.1 = 10.1
Sponsor Area
Mock Test Series
