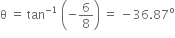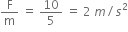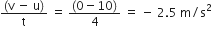Laws of Motion

Given,
Mass of the body, m = 3 kg
Initial speed of the body, u = 2 m/s
Final speed of the body, v = 3.5 m/s
Time, t = 25 s
Using the first equation of motion, 
                     v = u + at
Acceleration(a) produced in the body, a =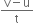
Therefore,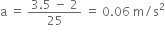 

Now, according to Newton's second law of motion, we have
F = ma
   = 3 x 0.06
   = 0.018 N
Since the application of force does not change the direction of the body, the net force acting on the body is in the direction of its motion. 

Mass of the body, m = 5 kg
The given situation can be represented as follows:


The resultant of two forces is given by, 
R = 
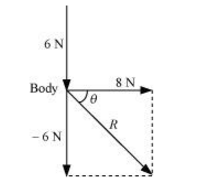
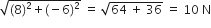
 is the angle made by R with the force of 8 N.
Therefore, 

The negative sign indicates that θ is in the clockwise direction with respect to the force of magnitude 8 N.
According to Newton’s second law of motion
Acceleration (a) of the body is given as, 
F = ma 
Therefore, 
a =

Final speed of the three-wheeler, v = 0 m/s
Time, t = 4 s
Mass of the three-wheeler, m = 400 kg
Mass of the driver, m' = 65 kg
Total mass of the system, M = 400 + 65 = 465 kg
According to the first law of motion,
Acceleration (a) of the three-wheeler is, 
                       v = u + at 

Therefore,
 a = 
The negative sign indicates that the velocity of the three-wheeler is decreasing with time.
Now, using Newton’s second law of motion, the net force acting on the three-wheeler is, 
       F = Ma

         = 465 × (–2.5)
 
         = –1162.5 N 
The negative sign indicates that the force is acting against the direction of motion of the three wheeler. 

Initial acceleration, a = 5 m/s²

Acceleration due to gravity, g = 10 m/s²

Using Newton’s second law of motion,
Net force (thrust) acting on the rocket is given by the relation, 
        F – mg = ma 

                 F = m (g + a)
                    = 20000 × (10 + 5)
                    = 20000 × 15
                    = 3 × 10⁵ N