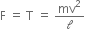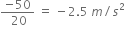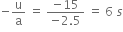A pebble of mass 0.05 kg is thrown vertically upwards. Give the direction and magnitude of the net force on the pebble,
(a) during its upward motion,
(b) during its downward motion,
(c) at the highest point where it is momentarily at rest. Do your answers change if the pebble was thrown at an angle of 45° with the horizontal direction?
Ignore air resistance.
A pebble of mass 0.05 kg is thrown vertically upwards. Give the direction and magnitude of the net force on the pebble,
(a) during its upward motion,
(b) during its downward motion,
(c) at the highest point where it is momentarily at rest. Do your answers change if the pebble was thrown at an angle of 45° with the horizontal direction?
Ignore air resistance.
The gravitational force is the only force that acts on the pebble in all three cases.
Its magnitude is given by Newton’s second law of motion as:
F = m x a