+91-8076753736 [email protected]
logo
logo

Laws of Motion

Question
CBSEENPH11020068
Wired Faculty App

A body of mass 0.40 kg moving initially with a constant speed of 10 m s–1 to the north is subject to a constant force of 8.0 N directed towards the south for 30 s. Take the instant the force is applied to be t = 0, the position of the body at that time to be x = 0, and predict its position at t = –5 s, 25 s, 100 s.
 

Solution

Given,
Mass of the body, m = 0.40 kg
Initial speed of the body, u = 10 m/s, due north
Force acting on the body, F = –8.0 N
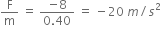
Acceleration produced in the body, a = straight F over straight m space equals space fraction numerator negative 8 over denominator 0.40 end fraction space equals space minus 20 space m divided by s squared
(i)
At t = –5 s,
Acceleration, a' = 0
Initial velocity, u = 10 m/s 
Using the relation, 
         s = ut + (1/2) a' t2 

           = 10 × (–5) = –50 m
(ii)
At t = 25 s
Acceleration, a'' = –20 m/s2 
Initial velocity, u = 10 m/s
USing the relation, 
            s' = ut' + (1/2) a" t2

               = 10 × 25 + (1/2) × (-20) × (25)2 

               = 250 - 6250
               = -6000 m
(iii)
At t = 100 s, 
For 0 ≤ t ≤ 30 s 
Acceleration, a = -20 ms-2
Initial velocity, u = 10 m/s
Now, using the equation of motion, we have
               s1 = ut + (1/2)a"t2 

                   = 10 × 30 + (1/2) × (-20) × (30)2

                   = 300 - 9000 
                   =  -8700 m
For 30 < t ≤ 100 s,
For t= 30 sec, as per the first equation of motion final velocity is given as, 

                   v = u + at 

                     = 10 + (–20) × 30
                     = –590 m/s 
Velocity of the body after 30 s = –590 m/s 
For motion between 30 s to 100 s, i.e., in 70 s: 
s2 = vt + open parentheses 1 half close parentheses a" t2 

    = -590 × 70
    = -41300 m 
∴ Total distance, s" = s1 + s2 
                          = -8700 -41300
                          = -50000 m
                          = -50 km.

Question
CBSEENPH11020069
Wired Faculty App

A truck starts from rest and accelerates uniformly at 2.0 m s–2. At t = 10 s, a stone is dropped by a person standing on the top of the truck (6 m high from the ground). What are the (a) velocity, and (b) acceleration of the stone at t = 11 s? (Neglect air resistance.)

Solution

Given, 
Initial velocity of the truck, u = 0
Acceleration, a = 2 m/s2
Time, t = 10 s
a)
According to the equation of motion, we have
                   v = u + at
                     = 0 + 2x10
                     = 20 m/s
The final velocity of the truck and hence, of the stone is 20 m/s.
At t = 11 s, the horizontal component (vx) of velocity, in the absence of air resistance, remains unchanged.
i.e.,                vx = 20 m/s 
The vertical component (vy) of velocity of the stone is given by the first equation of motion as,
                     vy = u + ay δt 

where,
δt = 11 – 10 = 1 s, and 
ay = g = 10 m/s2 

∴           vy = 0 + 10 × 1
                  = 10 m/s
The resultant velocity (v) of the stone is given as:
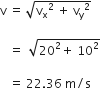
straight v space equals space square root of straight v subscript straight x squared space plus space straight v subscript straight y squared end root space space space space equals space space square root of 20 squared plus space 10 squared end root space space space space equals space 22.36 space straight m divided by straight s

Let, straight theta be the angle made by the resultant velocity with the horizontal component of velocity vx,
Therefore, 
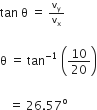
tan space straight theta space equals space begin inline style straight v subscript straight y over straight v subscript straight x end style straight theta space equals space tan to the power of negative 1 end exponent space open parentheses 10 over 20 close parentheses space space space equals space 26.57 to the power of straight o 
b) 
When the stone is dropped from the truck, the horizontal force acting on it becomes zero. However, the stone continues to move under the influence of gravity. Hence, the acceleration of the stone is 10 m/s2 and it acts vertically downward. 

Question
CBSEENPH11020070
Wired Faculty App

A bob of mass 0.1 kg hung from the ceiling of a room by a string 2 m long is set into oscillation. The speed of the bob at its mean position is 1 m s–1. What is the trajectory of the bob if the string is cut when the bob is

(a) at one of its extreme positions,

(b) at its mean position.

Solution

(a) When bob is at its extreme position:
The trajectory of the bob if the string is cut at one of it's extreme positions will be in vertically downward direction.
At the extreme position, the velocity of the bob becomes zero. If the string is cut at this moment, then the bob will fall vertically on the ground. 
(b) When the bob is at its mean position:
When the string is cut at its mean position, the trajectory of the bob will be a parabolic path. 
At the mean position, the velocity of the bob is 1 m/s.
The direction of this velocity is tangential to the arc formed by the oscillating bob. If the bob is cut at the mean position, then it will trace a projectile path having the horizontal component of velocity only.
Hence, the bob will follow a parabolic path. 

Question
CBSEENPH11020071
Wired Faculty App

A man of mass 70 kg stands on a weighing scale in a lift which is moving, 

(a) upwards with a uniform speed of 10 m s–1, 

(b) downwards with a uniform acceleration of 5 m s–2, 

(c) upwards with a uniform acceleration of 5 m s–2.
 
What would be the readings on the scale in each case?

(d) What would be the reading if the lift mechanism failed and it hurtled down freely under gravity?

Solution

(a) 
Mass of the man, m = 70 kg
Acceleration, a = 0
Using Newton’s second law of motion, we can write the equation of motion as, 
                      R – mg = ma

where,
 ma is the net force acting on the man.
As the lift is moving at a uniform speed, acceleration a = 0
∴          R = mg 
              = 70 × 10
              = 700 N 
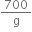
Therefore, reading on the weighing scale = 700 over straight g
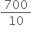
                                                     = 700 over 10
                                                     = 70 space kg
(b) 
Mass of the man, m = 70 kg
Acceleration, a = 5 m/s2 , downward
Using Newton’s second law of motion, we can write the equation of motion as: 
                      R + mg = ma 

                               R = m(g – a) 
                                  = 70 (10 – 5)
                                  = 70 × 5 
                                          = 350 N 
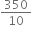∴ Reading on the weighing scale = 350 g = 350 over 10= 35 kg
(c) 
Mass of the man, m = 70 kg
Acceleration, a = 5 m/s2 upward 
Using Newton’s second law of motion, we can write the equation of motion as:

                        R – mg = ma 

                                 R = m(g + a) 
                                    = 70 (10 + 5)
                                    = 70 × 15
                                    = 1050 N
Therefore,
Reading on the weighing scale = 1050 over straight g
                                               = 1050 over 10
                                               = 105 kg
(d) When the lift moves freely under gravity, acceleration a =g 
Using Newton’s second law of motion, we can write the equation of motion as, 
                       R + mg = ma 

                                 R = m(g – a) 
                                    = m(g – g)
                                    = 0 
∴ Reading on the weighing scale = 0 over straight g= 0 kg 
The man will be in a state of weightlessness.

Sponsor Area

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation