Acids, Bases and Salts

The lens considered in the question is converging lens which is the convex lens. 

Given, 
Object size, h = 5 cm 
Object distance, u = -25 cm 
Focal length, f = 10 cm 

As the distances given in the question are large, so we choose a new scale where, 1 cm represents 5 cm. 

So, as per the new scale, 
Size of the object, h = 1 cm 
Object distance, u = -5 cm
Focal length, f = 2 cm.

The ray diagram can be drawn as follows: 

(i) Draw a horizontal line representing the principal axis of the convex lens.

(iii) Mark two foci F and F' on two sides of the lens, each at a distance of 2 cm from the lens. 

(iv) Draw an arrow AB of height 1 cm on the left side of lens at a distance of 5 cm from the lens. 

(v) Draw a line AD, parallel to principal axis and then make it pass straight through the focus (F') on the right side of the lens. 

(vi) Draw a line from A passing through the centre of curvature, which goes straight without deviation. 

(vii) Let the two lines starting from A meet at A' on the right side of the lens. 

(viii) Draw A'B', perpendicular to the principal axis. 

(ix) Now A'B', represents the real, but inverted image of the object AB. 

Using the lens formula,  

                     $\frac{1}{\mathrm{f}} = \frac{1}{v} - \frac{1}{u}$ 

$\Rightarrow$                 $$\begin{gathered} \frac{1}{\mathrm{v}} = \frac{1}{2}-\frac{1}{5} \\ = \frac{5-2}{10} \\ = \frac{3}{10} \\ v = 3.3 cm \end{gathered}$$ 

Also, we know that, 

              $$\begin{gathered} \frac{\mathrm{h}\text{'}}{\mathrm{h}} = \frac{v}{u } \\ \Rightarrow h = \frac{3.3 \times 1}{5} = 0.7 cm \end{gathered}$$

Since the image distance is positive, the image is real (formed on the right side of lens) at a distance of 3.3 cm.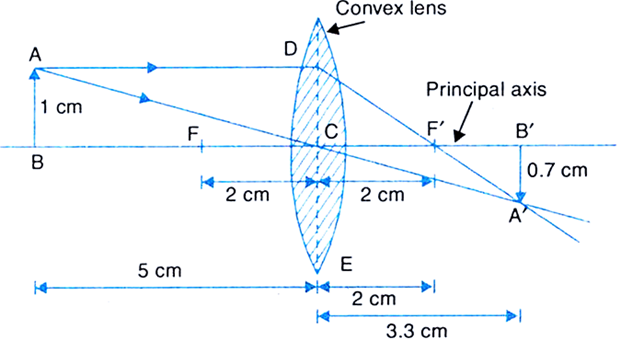 

Therefore as per the original scale, 

(a) Position of image A'B' = 3.3 cm × 5 = 16.5 cm from the lens on opposite side. 

(b) Nature of image A’B’: Real and inverted. 

(c) Height of image A'B': 0.7 × 5 = 3.5 cm, i.e., image is smaller than the object.

Given, a concave lens. 

Focal length, f = - 15 cm    [f is - ve for a concave lens] 

Image distance, v = - 10 cm [image formed is virtual i.e., on same side as the object, so v is - ve] 

Now, using the lens formula,

                     $\frac{1}{\mathrm{f}} =\frac{1}{\mathrm{v}}-\frac{1}{\mathrm{u}}$ 

                     $$\begin{gathered} \frac{1}{\mathrm{u}} =\frac{1}{\mathrm{v}}-\frac{1}{\mathrm{f}} \\ = \frac{1}{-10}-\frac{1}{-15} \\ = \frac{-3+2}{30} \\ = -\frac{1}{30} \end{gathered}$$  

Therefore, object distance, $\mathrm{u} = -30 \mathrm{cm}$ 

Ray diagram:

Inorder to make the diagram, lets use a scale where 5cm = 1cm. 
So, as per the new scale, 
Focal length, f = -3 cm
Image distance, v = -2 cm 

Steps to draw the ray diagram is mentioned below as follows:

(i) Draw a horizontal line which is called the principal axis. 

(ii) Now, draw a convex lens keeping principal centre (C) on the principal axis. 

(iii) Mark points F (focal length) and B (image distane) on the left side of lens at a distance of 3 cm and 2 cm respectively. 

(iv) Draw a dotted line passing through F to any point on the top of the lens, say D. 

(v) So, we can draw a line AD parallel to principal axis because any ray of light passing through the focal length of the lens after refraction, passes parallel to the principal axis.

(vi) Draw a line A'B', perpendicular to principal axis from B' representing the height of the image. 

(vii) Draw a line CA' backwards, so that it meets the line from D at A. 

(viii) Now, draw a line AB, perpendicular to the principal axis at B from point A in the downward direction.  

(ix) AB is the position of object. On measuring distance BC, it will be found to be equal to 6 cm. 

Thus, the object is placed at a distance of 6 cm × 5 = 30 cm from the lens (as per the original scale).

Given, a concave lens. 

Focal length, f = - 15 cm
Image distance, v = - 10 cm [Concave lens forms virtual image on same side as the object, so v is - ve] 

Using the lens formula,

                          $\frac{1}{\mathrm{f}} = \frac{1}{\mathrm{v}}-\frac{1}{\mathrm{u}}$ 

$\Rightarrow$                     $$\begin{gathered} \frac{1}{\mathrm{u}} = \frac{1}{\mathrm{v}}-\frac{1}{\mathrm{f}} \\ = \frac{1}{-10}-\frac{1}{-15} \\ = \frac{-3+2}{30} \\ =-\frac{1}{30} \end{gathered}$$ 

Therefore,
Object is placed at a distance of 30 cm ( negative) from the lens. 

The ray diagram is as shown below:  


 

AB is the position of the object.

We are given a convex mirror. 
Here, 

Object distance, u = -10 cm 
Focal length, f = + 15 cm [f is +ve for a convex mirror]
Image distance,  v = ? 

Using the mirror formula, 

                     $\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{v}} = \frac{1}{\mathrm{f}}$ 
we have, 

$\therefore$                  $$\begin{gathered} \frac{1}{\mathrm{v}} = \frac{1}{\mathrm{f}}-\frac{1}{\mathrm{u}} \\ = \frac{1}{+15}-\frac{1}{-10} \\ = \frac{2+3}{30} \\ =\frac{1}{6} \end{gathered}$$ 

Thus, image distance,  v = + 6 cm.
 
As image distance is +ve, so a virtual, erect image is formed at a distance 6 cm behind the mirror.